Antiracist teaching strategies: the Tug-of-War task

Summer, 2023

Some might think being antiracist is about confronting overt racism in curriculum or school policies but there is much more to it. Being antiracist as a math teacher is about recognizing how hierarchical power dynamics in the classroom mimic the ways bias and racism operate in our society. Ibram X. Kendi claims, “Becoming antiracist requires every individual to choose every day to think, act and advocate for equality, which will require changing systems and policies that may have gone unexamined for a long time.” (Schwartz, Interview with Kendi, 2019). Therefore it is antiracist in practice if math teachers act for equality by changing teaching practices and classroom policies that have long gone unexamined, actively shifting the power dynamic from teacher in control of students to one where learners, including the teacher, are in control of the learning together.

The Tug-of-War task is one of many that can be used to practice antiracist teaching strategies in the math classroom. What characterizes this task as a worthwhile option is the openness of the task, the lack of a prescribed solution pathway, and the easily accessible and relatable context. This task is adapted from a unit of study called Math In Context: Comparing Quantities (pp. 3, 2003) for middle grades. The unit is an introduction to algebra and explores several strategies to determine unknown quantities. All the standards for mathematical practices (SMP) could be explored through this task, but especially SMP 1, “Making sense of problems and persevere in solving them.” Antiracist teaching strategies in the math classroom are those that empower all learners to take the lead in sense-making, recognize the brilliance in one another, and break the cycle of sorting and filtering students based on racial identities and perceived abilities. In this article, antiracist teaching strategies are described in the context of facilitating this task through the launch, student work analysis, and whole group discussion.

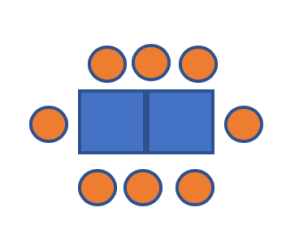
Figure 1: The task

Launch

A typical launch might involve a teacher explaining a concept or steps to follow. Instead the teacher can launch this task with a few words and puzzle alongside students. The image in Figure 1 is displayed on a shared visual space, e.g. projected on a whiteboard and students are asked who has played tug-of-war before. The teacher is not explaining the image nor are they describing the work product yet. Spending time on establishing a clear and shared understanding of the game itself is crucial to developing a deeper sense of mathematical equality in this context – when there is a tie there are no winners and both sides are balanced in strength. This adaptation removes the names of the animals and statements of equality from the original task (e.g. “four oxen are as strong as five horses”) and replaces them with shorter phrases e.g. “it’s a tie!”

It is important to remain neutral during the launch and check for understanding from all students. The teacher should avoid sharing their own noticings disguised as questions, e.g. “Do you all see that the elephant is the strongest?” The teacher must refrain from confirming or disconfirming any responses to what students conjecture is the problem to solve. For example, students may ask “Isn’t the elephant the strongest?” or “Isn’t the third one a tie too since it’s four animals versus four animals?” Some examples of a neutral response are “What do others think?” or “What makes you think that?” or better yet, nodding and remaining silent and simply letting people think about what was said. Students should not raise hands and share in the whole group until there has been sufficient time to work independently and in partners. Often there are known “smart” students in the classroom and once they speak, other students may shut down and disengage with the problem. Ilana Horn (2012) calls this a “status hierarchy” where the “smart” students are assigned more power than others in the classroom and could inadvertently control the pace of learning in a lesson. Instead, the teacher can consider asking all partnerships to contribute noticings and conjectures to the group conversation after everyone has had sufficient time to think.

The launch strategies above challenge the belief that the teacher is the source of control and knowledge and that some students are meant for math and others are not. When the teacher remains neutral in the launch the message is sent that everyone’s contributions are worthwhile and the teacher is positioned as a member of the problem-solving community, effectively saying, “I am with you in this effort.” Practice can shift away from the typical one-way dialogue between a teacher and student and instead invite discussion from all others in the space. The launch ends with articulating the question, “Who wins the final tug-of-war?”

Analyzing Student Work

To orchestrate a meaningful discussion about different solution pathways, student work is collected, analyzed, and then presented back in a sequenced order on the following day (Smith & Stein, 2018). The learning target in this instance is to represent scenarios using equations and variables and construct viable arguments connecting the strategies presented. (HSA.SSE.1: Interpret expressions that represent a quantity in terms of its context. HSA.REI.1: Explain each step in solving a simple equation as following from the equality of numbers asserted at the previous step, starting from the assumption that the original equation has a solution. SMP3: Construct a viable argument to justify a solution method.) In the ninth grade class from which the sample work is taken, a total of eight artifacts were collected and three were chosen to display during the whole group discussion.

There are two connections across the three samples worth drawing out to support the learning goals. First, the strategies for working with equality are different. In Samples 1 and 2 the solution paths differ in terms of assigned values. In Sample 1, the values are assigned for each animal first (an ox is worth 4 and a horse is worth 5) and in Sample 2, the value for equation 1 is decided first (100=100) and then the values of oxen and horses are derived. Second, in samples 1 and 3, the authors model the animals but in different ways. In Sample 1, the animals are represented pictorially and in Sample 3 the equations are modeled using variables (see pink text). Comparing these two samples of work provides an opportunity to connect the pictorial representation of four oxen with the value “4x”, five horses with “5y”, and so on.

Studying student work and selecting samples to discuss in a specific order is a departure from the practice of grading student work and handing it back. Grades have long served in the process of ranking and sorting students by performance (Deshpande, 2015). In this process, students are not given grades after the first day and instead are invited into the process of giving feedback for the purpose of learning on the next day. Lesson planning in this instance involves strategizing how to highlight student voice, empower students to make their own mathematical connections, and shift practice away from using a textbook to using student work as curricular material.

Sample 1: Substitute values for animals in first equation

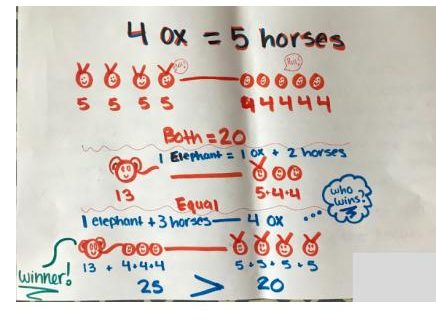
Sample 2: Set sides equal to a value in first equation

Sample 3: Model with equations

Whole Group Discussion

The second day begins with projecting work samples on the board and discussing them one at a time. To keep track of ideas the teacher should document the connections students are making on the board and try labeling ideas with the students’ names. The small step of assigning student names to their ideas can bolster confidence and confirm that students are contributing members of the math community. As predicted, the students connected “4x” and the drawing of four oxen and “5y” to the drawing of 5 horses, as follows in Table 1. Finally, the third tug-of-war is assessed in two ways, by substituting the values from Sample 1 (outcome 25>20) and Sample 2 (outcome 125>100) into the equation from Sample 3 which is z + 3y ≠ 4x. Spoiler alert: one elephant and three horses are stronger than 4 oxen (z + 3y > 4x).

Table 1: Making connections between pictorial and algebraic representations

In this particular instance, what happened next was not predicted! The students pushed the conversation into modeling substitutions and observing multiplier effects, see Table 2. Students worked with two equalities and three variables, deepening their understanding of how quantities can vary in proportion to one another in linear systems of equations. This was also a perfect opportunity to model using a table to keep track of student observations. By the end of crafting the table, some students asked a new question, “What are all the possible values of x, y, and z?” Ultimately, the students met the learning goal to model with equations and variables by the end of the lesson and furthermore ended with a new question to explore. A robust and lively discussion took place in which students were doing the “heavy lifting” to make connections across representations.

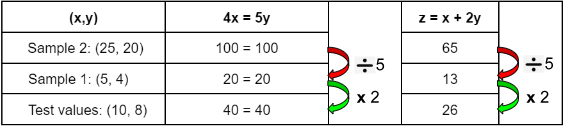
Seeing multiple ways to solve the same mathematics problem not only builds students’ problem-solving toolkits but also requires that students and teachers acknowledge and honor each other as equals on a level mathematical playing field. It has been shown time and again that students of color largely receive a subpar education as evidenced by persistent gaps in academic outcomes and access to opportunities (e.g. Mervosh & Wu 2022) so it is of the utmost importance that teachers practice the skills necessary to treat all students in their classrooms equally and fairly. The reader might ask, how is this considered antiracist especially if a teacher is teaching in a racially homogenous classroom? The answer is that classroom practices do not happen in a bubble, and how different abilities and approaches in the math classroom are honored is parallel to how the contributions made to any community e.g. workplaces, neighborhoods, cities, etc. by persons of any race, nationality, (dis)ability status, gender orientation, and other social identities are honored. According to Kendi (2023), antiracism is about shifting from focusing on the individual or group to focusing on the outcome, so the focus in this moment is on honoring how solution pathways can be vastly different and the result is the same, equal outcome.

Conclusion

Being antiracist is about challenging any policies and practices that position people in false hierarchies. It is not always about confronting overt forms of racism. By engaging in antiracist teaching, teachers can confront long-standing biases against various communities of color by questioning their assumptions and making good faith efforts to employ some of the strategies described above. Practicing antiracism in teaching is about practicing how to genuinely honor and value students’ contributions regardless of their racial backgrounds, past performances, or perceived abilities in math.

References

Boaler, J. (2015). Mathematical mindsets: Unleashing students’ potential through creative math, inspiring messages and innovative teaching. John Wiley & Sons.

Deshpande, A. (2015). Making the Grade: Exploring the variability of grades and teacher beliefs about grading in New York City public middle schools. Doctoral Dissertation. New York University.

Driscoll, M. (1999). Fostering algebraic thinking: A Guide for teachers, grades 6-10. Heinemann.

Emdin, C. (2016). For White folks who teach in the hood… and the rest of y’all too: Reality pedagogy and urban education. Beacon Press.

Freire, P. (1970). Pedagogy of the oppressed. Herder and Herder, New York.

Goffney, I., Gutiérrez, R., & Boston, M. (2018). Rehumanizing mathematics for Black, Indigenous, and Latinx students. National Council of Teachers of Mathematics.

Horn, I. S. (2012). Strength in numbers. National Council of Teachers of Mathematics.

Kendi, I. X. (2023). How to be an antiracist. One world.

Love, B. L. (2019). We want to do more than survive: Abolitionist teaching and the pursuit of educational freedom. Beacon Press.

Mathematics in Context: Comparing Quantities. (2003). Holt, Rinehart, & Winston.

Mervosh, S., & Wu, A. (2022). Math scores fell in nearly every state, and reading dipped on national exam. New York Times.

Schwartz, K. (2019). Interview: How Ibram X. Kendi’s definition of antiracism applies to schools. KQED.

Smith, M., & Stein, M. K. (2018). 5 Practices for orchestrating productive mathematics discussion. National Council of Teachers of Mathematics.

Invasions and Invitations

Lately I have had several conversations with colleagues and friends about implicit bias and racism. As a scholar of race and schools, and specifically urban education, I am drawn to studying ways that beliefs impact practice. The topic of microaggressions comes up often in my conversations.

Some people are well-versed in what microaggressions are, and can share anecdotes either from their own lived experiences or experiences shared by peers. Others are in a beginning place about the concept and might be skeptical — they can recognize overt forms of racism (hate speech, violent acts) but cannot yet see how a seemingly innocuous compliment is actually a microagression. For instance, I have received compliments about my hair that are veiled inquisitions unto my body: “your hair so so different and pretty! Is it like that naturally, or to you have to do something to it to make it so curly? Can I touch it?” Sometimes the question is left off, and I have had others touch my hair without asking permission. In another instance, I was asked if I “really see myself as a woman of color.” This translates to the classic “you’re so articulate for a person of color” transgression, the sting was much worse because it came from a close and trusted colleague.

An invasion is when someone does not take social cues and assumes the right to ask about another person’s cultural heritage and background or (as in the case of my hair, will go so far as to touch me without permission). An invitation, on the other hand, is the act of inviting a conversation about one’s identity and lived experience. An invasion is like pushing through a door to walk through it, whereas an invitation involves a person coming to the door and opening it for another to enter. As a scholar of urban schools, I’ve been thinking about the types of microaggressions students deal with on a daily basis. I worry about these microaggressions because children do not always have the conversational tools or vocabulary to challenge an adult in a way that sheds light on the microaggression. Children are experts in understanding fairness, and can sense when questions and comments do not feel fair or out of bounds, but often don’t know exactly how to speak up about how something makes them feel.

Below are two examples of exchanges in which a caring adult interacts with a student on the basis of getting to know one another a little bit better. The first is a a conversation I recently heard between a well-intentioned white adult and a ninth grader who is a person of color.

Adult: What’s something you like about being in this school?
Student: We don’t have homework at this school! It’s great, I had way too much homework at my old school, I just moved here.
Adult: So, where are you from? And where’s your family from?
Student: Harlem. Now we’re in Brooklyn.
Adult: Oh, that’s quite a distance to travel to get to school in Manhattan. But where is your family from?
Student: Uhh, yea it’s pretty far I guess. My family is from Mexico.
Adult: Okay! That’s so great!

(conversation ended here)

Compare the above with the invitation below. In the conversation I heard, a well intentioned white adult had a conversation with a student of color at the same school as above, and with the same goal of getting to know one another a little better.

Adult: So what’s your favorite food?
Student: I really love Caribbean food, it’s delicious.
Adult: Oh, I really enjoy Caribbean food. I really like eating the seafood curries, I wish I knew more about Caribbean cooking. What’s your favorite Caribbean dish?
Student: I love eating everything. I especially love my mom’s jerk chicken and rice. She is from Jamaica.
Adult: Oh, okay! Your mom is from Jamaica, do you have family there?

(conversation continues until student passes to lunch in the cafeteria)

An invitation feels natural and builds a bridge between people. When an invitation goes well, sometimes the question about one’s cultural or ethnic heritage might not be needed because the information is raised naturally in dialogue (“She is from Jamaica.”). An invasion is usually met with discomfort or confusion on the part of the student, who is likely to find themselves* in a precarious situation. Power and status hierarchy are at play. A student has to consider the risk imposed if they are seen “talking back” to the teacher/adult in the situation, so the least harmful course of action is to remain neutral and safely exit the conversation with a slightly awkward moment. The most harmful course of action could result in punishment if the student’s response is unacceptable to the adult.

When a student offers information about their identity, slow yourself down and check in with your preconceived notions about that student — we all have them, it is what you do about your preconceptions that will make the difference. Then, pick up on the invitation. Stay on the subject, don’t overgeneralize, and share enthusiasm if you genuinely feel it. Avoid empty praise and gratitude (“That’s so great!”) and do not assume to know more than what is offered. In the second exchange, it would have been a mistake to say, “Where is your dad from?” because that isn’t information the student has offered for the discussion. If as educators, you are able to actively engage and practice authentic conversation with young people, you may find that you experience a shift in your preconceptions about people, and your actions may begin to more wholly support your beliefs about equity and equality.

In the math classroom, invitations and invasions look similar. In one instance, an eighth grade student of color responded to a question posed to the whole group about what they noticed in a table of values. The table contained information about incomes for men and women in the United States. When the student shared that incomes for men are “much more greater by almost double,” the teacher interrupted the student prematurely and then only recorded the word “greater” on the board as his noticing. The student is of West African decent (I know this because I have had conversations with this student) and speaks with an accent. The teacher did not slow down to hear the most important mathematical contribution the student made, he observed one value is nearly double of another. The teacher committed an invasion by interrupting the student, and as I learned later, this invasion was intentional because the teacher felt as though they were not going to understand what was said next. In that moment, I raised my hand to get some clarification on what I heard, and the teacher updated the student noticing to state, “greater, almost double.” This moment was troubling to me for two reasons. First, how will the teacher learn that what they did was silencing to the student, and did my actions do anything to help the student speak for themselves? I used my power and privilege in the classroom as a math coach and I knew I would be called on immediately and that my contribution would be heard and recorded. In this case, I followed up with student and teacher about the moment afterwards, but how many of these interactions go unchallenged?

In my separate debriefs with the teacher and student we talked about strategies that could be used to slow down in the teacher’s case and speak up in the student’s case. The teacher admitted to being a little confused by the student’s accent, and we talked about how to slow down to help avoid an invasion, and ask for students to repeat themselves loudly so that they are heard. It is okay to say, “I didn’t hear you, can you please repeat that?” Research shows, unsurprisingly, that by listening to an accent that is different from yours for longer periods of time, your brain maps the words you hear onto the words you already know and comprehension improves. And just think about the types of invitations that may occur as you hear your students speak freely with you! The lesson is, listen to your students more. For my debrief with the student, I asked them how they felt when they were misunderstood, and the student shared feelings of confusion and sadness. We talked about how it is okay to say, “that’s not exactly what I said.” It is not a perfect strategy because it does not level the power structure between teacher and student, but it does at the very least give more voice to the student for a brief moment.

We cannot go through with our daily work feeling proud of our equity-based stance on mathematics education, it is not enough and we must actively work on changing our preconceived ideas about groups of people who are different than us. Well-intentioned educators of various racial, ethnic, gender, and other social identities commit microaggressions and invasions all the time. In my experience, and largely in the literature on microaggessions, invasions are more frequently committed by people from the dominant culture – straight, cisgender, financially stable, white people, however, nobody is off the hook. What I propose in this blog is that there is a great need for math educators to actively practice engaging in and picking up on invitations into dialogue with students, because students in most instances do not have the power or privilege to challenge invasions levied upon them. To avoid committing invasions my advice is simple — slow down, check in with preconceptions, and listen with care.

*Non-binary pronouns are intentional.

They Can Fit

I was working in a middle school classroom in Harlem on a problem called “chairs and tables.” It is a classic problem:

The Italian Villa Restaurant has square tables that the servers can push together to create longer tables and seat larger groups of customers. One one chair fits along a side of the square table.

Students were invited to model the problem using flat tiles and dried black beans. Each bean represented a person in a chair and each tile represented a table. Students played with the model for a little while and shared how they would lengthen tables and add more chairs. Here is an example of how one child thought about the problem:

student work tables and chairs.png

As seen in the image, the student envisions moving the chair on the right around to the side of the second table, adding two chairs to the top and bottom of the second table, and then the tables get “put together.”

Students worked on solving and creating an algebraic rule for the problem, based on building the model and then keeping track of the data on growing patterns in a t-chart. Most students found the rule 2t + 2, where t=tables. The purpose of the task was to model a pattern and make the leap to algebraic representations for tables of any length.

I could go on and on about marvelous and brilliant student strategies for solving this problem. The most important moment in working on this lesson for me as an educator took place during a conversation I had with one student named Damon. Damon was perplexed by this problem and struggled to model the addition of a square table to the existing table. To step back a moment, I started the problem by having students share about a time that they went out to a restaurant to eat with their families, and we talked about how sometimes we might see the servers moving tables together so that families could be together. To Damon, this problem presented a challenge that did not match his lived experience and caused an obstacle to seeing the problem as described.

Damon worked and worked, and kept adding four chairs every time he added a table. I asked him to restate the rule governing the problem, that there could only be one chair on one length of the square. But Damon insisted, “just put the extra person between the tables, they can fit.” To Damon, it was unthinkable that the servers would leave two people out every time they moved tables together. When we described the problem and asked students to envision the act of putting tables together, Damon envisioned his family and he was not thinking in chairs and tables, he was thinking about people. If there are already people sitting around a table, and then we want to slide tables together, to him it would be impossible to leave out the people on the ends and the servers should squeeze everyone in. For two tables, Damon drew this:

What I learned in that moment is that context and clarity really matter, especially if we want students to connect to the mathematics and grow their critical thinking skills. This problem in the most academic form is a standard linear growth problem — for each table add two chairs. Damon’s interpretation of the problem based on my explanation of families going to dinner together led him to see the problem in a different and beautiful way. Damon needed to include everyone, because that’s what happens in his family. I am indebted to Damon and the light he shined for me that day. I learned that how I talk about a problem needs to be clear — if I clearly talked about adding chairs before the family sat down together to eat, I wonder if Damon would have made sense of the context that I planned for. Second, I reflected and thought about how for some students who come from families and cultures that focus on inclusion and community, these types of problems that rely on shared cultural norms may not be interpreted in the same way when our cultural norms and beliefs vary. Can I go so far as to say this is evidence of a colonized curriculum in mathematics? Probably not. But I am pausing to think about how I can blur the lines between “school math” and reflecting students’ lives purposefully in the mathematics curriculum.

As a woman of Indian cultural heritage, I too can relate to how Damon understood this problem. For some communities and cultures, the norms around eating and communal gathering dictate that everyone should be included; and we can always say, “they can fit.” Growing up in an Indian family, our outings and social gatherings always included everyone, the elderly, the children, and the parents. We did not leave anyone out, and if we needed to move a little this way or that way to ensure everyone had space to sit and eat at a table, we did.

The conversation with Damon was so powerful for me because I could draw a distinction between an academic interpretation of the chairs and tables problem and the reality of children and families from diverse cultural backgrounds going out to eat. I continue to wonder about how to bring in more context from students’ lived experiences to add richness and love to the math classroom. When children feel that their lives are reflected in the content in math, they are more likely to engage and persist in problem-solving. I will be more careful in the future, as I think about the tables and chairs problem and other problems like it.

Socio-Politics of Numeracy

The Socio-Politics of Numeracy: What 6th Graders in the Bronx Wonder About

By Anjali Deshpande and McKenna Shaw

In February, 2018, McKenna’s school participated in New York’s Black Lives Matter Week of Action In Schools. This middle school is located in the north Bronx and serves a diverse student population, with the large majority of students qualifying for free and reduced price lunch. Many students’ families are living in poverty. The school’s administrative team ascribes to progressive ideals about community, service, and citizenship. The teachers work very long hours, often working weekends and nights. Similarly to other Bronx middle schools I’ve worked in, the students are almost all Black and Brown, and the school is subject to a revolving door of reforms that are implemented and sometimes abandoned in place of new policies. While it is a safe and welcoming environment, the school continues to look for ways to support students with diverse learning needs.

To start to the week of action, McKenna and I revisited the Black Lives Matter Guiding Principles and reflected on how the principles spoke to the reasons we became educators. I helped McKenna find a way to open the unit of study by asking her 6th graders: “What connections do you see between Black Lives Matter and our work in Math and Science?” This question was met with silence, blank stares, and one or two cocked heads and raised eyebrows. Then we asked students to write. We received numerous reflection papers where the sentence starter, “A connection between math and science and Black Lives Matter I see is . . . “ went unfinished. Several question marks, a few doodles. We received a limited number of substantial responses, one student wrote, “All of us in the classroom, we are a family,” and another wrote, “ one of the principles was called a ‘village’ meaning people coming together to make a family larger than your own.” Some students shared that they felt safe to make mistakes in math and science, and have their questions answered. Students saw McKenna as a teacher who “had their back” and would advocate for them socially and academically.

We learned two things. On the one hand, McKenna had created a safe classroom environment where students could engage respectfully and appreciatively of the diverse identities in the room. Students recognized and named the enactment of many of the Black Lives Matter principles in the classroom. It was rewarding to hear from sixth graders that they feel safe to learn especially when some students are coming to school to escape potentially difficult conditions at home. But it was evident that the students did not yet see math and science as real tools that can be used to measure, discuss, and affect social and political change. “Math politics? Is that a thing?” one student asked.

Mathematical literacy, or numeracy, must be primary goal for our students, it is a requirement for justice and citizenship. PISA (2013) defined the mathematically literate person as “one who understands the role mathematics plays in the world, makes well-founded judgements and uses mathematics to meet their needs as a constructive, concerned, and reflective member of society.” In Horace’s Compromise, Ted Sizer (1984) claims “Numeracy means the ability both to use numbers, arithmetically and algebraically, and to understand the concepts, relationships, and logic embedded in mathematical thought. A modern citizen cannot make critical judgments without these skills.” The math curriculum at the school asks students to reason mathematically with real-life contexts, and while using unit rates at the grocery store to identify a better buy is important and necessary, the curriculum is not designed to push students to become mathematically literate and empowered to make critical judgments about their worlds. Calculation is not enough.

In retrospect, McKenna and I are thinking of ways to shape next year’s statistics unit around current events. What better place to help students see the real and powerful applications that math has in the socio-political world? McKenna decided to pilot a new routine this year. She introduced the graph “Gun Deaths in Florida” and created a space for students to ask questions, think critically, and make connections. Take a moment toanalyze this graph; notice the y-axis (vertical axis) is inverted and the values decrease from bottom to top. Did you think gun deaths went down prior to “Stand Your Ground” law? At first, so did we. After having a chance to unpack features of the graph, one student asked, “Wait – wasn’t Trayvon Martin killed in Florida? What year was he murdered?” Trayvon Martin was killed in 2012, and it was powerful to hear a sixth grader ask this question because this student was making an important connection. A great math lesson about interpreting graphs will help students make sense of data, but an empowering lesson about graphs will motivate a student to research, question, analyze, and critique the way things work in the world.

McKenna is now reflecting on the power to build numeracy into her daily teaching and learning practice. Rather than saving rich content for the very last unit of the school year, where statistics usually lives in the sixth grade curriculum, she plans to make “Math in the News” discussions happen once a week. Even if these discussions last for 5-10 minutes, the hope is to establish the norm of discussing politics, social justice and awareness, and news in math class. The hope is to help students ask the most important questions about their worlds. Students today find themselves in politically charged spaces, take the #Enough movement and gun control walkouts for example, and it is our job to give them the tools, critical and analytical skills, and the language they need to affect change. Instead of teaching math as a “school” subject and hoping students will make connections outside of the classroom, we must make space for those connections to happen during the school day.

Using Exit Slips

How a More Thoughtful Approach to Exit Slips Improved my Teaching

Like so many teachers, I wrap up a lesson and with a few minutes left in the period, I hand out my exit slips. My students work quickly and quietly to jot down their solutions. As students finish up, I move around the room and pick up their slips, meanwhile the students pack up. Class ends, students leave. It’s now my prep period, so I sit down and scan and sort my exit slips and I track the results. I have just the right information I need about student learning and I make a quick adjustment to tomorrow’s lesson plan. Using exit slips seems simple enough, right? Not quite. There is much more to the theory and practice behind using exit slips to inform high quality instruction.

Exit Tickets As Both Formative and Summative Assessment

A critical component of lesson planning is assessment, and most of us know that assessments generally fall into two categories, formative and summative. Formative assessments are those that take place along the way, inform instruction, and are typically low-stakes (e.g. agree/disagree talk moves, listening in on students during Turn and Talk, etc.). Summative assessments provide summary information, or evaluative data at the end of something like a unit or semester of study. Common summative assessments are exams and final projects; they are typically hands-off style evaluations that are used to inform student grades. This article focuses on one type of assessment, the exit slip, that I have used as both formative and summative depending on my assessment goals.

Robert Marzano, a leader in the field of assessment, focuses on using exit slips to provide feedback on a teacher’s instructional practice in four ways using; prompts that provide formative feedback (How much of today’s lesson did you understand?), prompts that stimulate student self-analysis (What could you have done differently today?), prompts that focus on instructional strategies (How did group-work help you understand the content today?), and prompts that are open communication to the teacher (What’s something I can be doing to improve your understanding of the content?). In addition to these reflective prompts, it is important to use low-stakes opportunities for quick feedback to gauge how well students have understood new content, especially in math and science, where content builds in hierarchical ways. For example, knowing how to find equivalent fractions is foundational to thinking about fraction operations, and being able to use the powers of ten really aids in student understanding the laws of exponents. In the following, I list the different types of exit slips and when it’s best to use each one.

Three Types of Exit Slips

In my practice, I use three types of exit slips. The language I use may vary depending on the age group and literacy needs of the students I’m working with. While this article is about exit slips in the math classroom, they can be used in different subject areas as well. Each type of exit slip is useful in different situations.

Open ended reflection: Open ended exit slips are generally a list of two or three questions designed to have students reflect on what they learned and what they may have questions about. Some of Marzano’s exit slip types fall into this category. I like to use the open-ended reflection exit slip on days when I’ve covered a lot of new information, or when we are in the middle of working on a project, or if I’m not sure how much of the lesson my students grasped. One important note: If possible, I recommend leaving visual displays of learning available to students during this reflection, because this one is not about informational or procedural recall. Rather, it’s about getting students’ feedback on my lesson. They may want to refer to something specific if they aren’t sure what the learning experience was about.
Individual Effort and Participation: Social emotional learning and self-regulation are critical 21st Century skills. We as teachers can do a lot to reinforce key ideas and skills by embedding social-emotional learning opportunities in our lesson plans. For this type of exit slip, I like to use something like a participation check-in (see Image 1 for an example). Students rank themselves for the day and include a sentence or two about why they scored themselves the way they did. I track this data and will often write back to students especially if I see an opportunity to provide specific and actionable feedback. By asking students to rank themselves, I can hold students accountable to being active and present during class. This practice also brings student voice into the process of evaluating participation.
Content: Have you ever ended a lesson and thought, “I nailed it!”? One way to confirm you hit a specific learning target (see Susan Brookhart’s work for more on learning ) is to use a content exit slip. I typically use one or two questions and pre-print these on half sheets or quarter sheets of paper (though posting the questions using a Powerpoint or something like it is fine too). Content exit slip questions can be something like, “Write four equivalent fractions for ⅔ and show your thinking” or “Use the distributive property to solve 72 x 5.”

Purpose and Equity

Many high school classrooms have short 45-minute periods for math class, and sometimes teachers have 120 students or more to work with, so grading daily assignments can become impossible. An exit slip is quick! Using an exit slip can help teachers remain focused on the topic and unit of study, and it helps to get feedback from the students as you go along. Unlike the state exams, exit slips can be given back to students and used as a teaching tool or an “assessment for learning” (Black et al., 2004). This is particularly important in places like New York City, where too often we are teaching in classrooms with students who have not had the same access to opportunities to learn, and we are still asked to measure their learning using high stakes tests. Exit slips are less intimidating and time-consuming and actually serve the purpose of giving teachers important information about what students know, what confuses them, and where we should go next in our teaching in a very timely manner.

Exit slips also add a layer of democratic participation to my classroom. It is not uncommon for teachers to feel so committed to pacing guides and curriculum maps that we teach through student confusion for the sake of completing the plan. Students voices are drowned out as teachers rush through the lessons. Exit slips are a way to slow down, refocus at important points in the learning journey, and take in important information from our students about what they need to learn next. Ilana Horn (2012, pp. 56-57) identifies four ways that assessment for learning supports the type of equitable mathematics teaching that incorporates student feedback. Assessments for equitable teaching (1) emphasize learning over achievement, (2) provide information that informs instruction by design, (3) are non-punitive (i.e. not a missed opportunity to learn), and (4) allow student voice to impact what comes next. Using data gathered from exit slips helps me show the students how deeply I care about their learning and well-being. Exit slips are powerful tools, and when used the right way, they can help develop trust and safe learning spaces for students.

How to Use Exit Slips

A key feature of exit slips in the math classroom is that they cannot be graded or included in grade calculations. Instead, I use a simple roster with students names and exit slip topics to track data and observe patterns. I recommend that you scan your data over time to see which students are grasping new content, how students’ self-reported participation scores ebb and flow, or whether the students are more receptive and engaged with certain lessons than others. Sometimes data can be overwhelming, using a roster or another tool to track student outcomes need not be a burden. The point is to study the trends — the act of making yourself aware of trends in data will inform your practice in subtle and important ways.

Sharing marked content exit slips with students is great when done properly. You will find that several students will want to revise and resubmit their exit slips for various reasons. It may be the case that students made a silly mistake and want you to see how they knew what they were doing. It may be that something clicked after class ended, this is ideal because it suggests that students continued working and thinking. In fact, the quick feedback and opportunity to revise may go a long way to improving retention of new information. I recommend holding back on returning content exit slips if you did not have enough time to provide feedback that helps students think about the next step in learning a topic.

We have all worked with students who can’t bear the thought of losing points, and for these performance driven students, the exit slip will take longer to get used to because it doesn’t involve grading in any way. It is worth sustaining a dialogue with these students to help them think about the importance of productive struggle and adopting a growth mindset. I recommend that you review the exit slip protocol (see example ) a few times with your students, because exit slips are similar to tests in terms of working independently and quietly, but they are completely different in their purpose, and this takes time to get used to.

Exit Slip Protocol

Do’s

When launching exit slips, you might say something like, Now we’re going to switch gears to our exit slip protocol. Remember, exit slips do not affect your grades (if applicable, say “and you will get them back tomorrow”). I use exit slips for a few reasons, sometimes I like to see what you’ll do with a new problem and sometimes I want to find out about your successes and challenges. I am interested in learning about how you think mathematically! Exit slips help me improve my teaching. If you get stuck, that’s okay, you can write to me about what you understand and what questions you still have.
Keep the exit slip free of distractions and prepare the students ahead of time with a discussion about the purpose of the exit slip. Include student voice by taking the time to explain how exit slips work to improve teaching and learning, and encourage your students to make sense of the process with one another.
Exit slips are short. If they get too long, then they are not exit slips, they are something else. A rule of thumb that I share with teachers I coach is that an exit slip should take two to four minutes to complete. The benefit of a short exit slip is that you can count on student engagement and effort for a short burst more confidently than say, for a longer quiz or test. The point of the exit slip is to be transitional, a brief moment-in-time assessment.
Exit slips need not be fancy, since some of the time, you’ll throw exit slips away after recording the data. You can even ask students to write their thinking on a piece of lined paper and put the exit question(s) on a slide.

Don’ts

Don’t use an exit slip as a quiz grade. Be very clear about what the exit slip is for, and it’s many benefits.
Don’t take away an exit slip if you notice a student looking at another student’s paper. Instead, you may want to have a follow-up conversation with the student about what prompted the behavior. It’s important to encourage students to be silent and work independently. After all, students are under tremendous pressure to succeed and want to get things right the first time! It takes time to develop a culture centered on assessment for learning and not performance.
Don’t give an exit slip as a punishment. It will taint the process and jeopardize the trust you have built with your students, especially if you have clearly stated that exit slips are about the learning process.

Conclusions

Exit slips can improve how you make sense of what your students need next. In my practice, I use three different types of exit slips; reflections, effort and participation, and content. Exit slips are critical reflections of my practice and by analyzing patterns in student responses, I’ve been able to revise my teaching strategies for the better. I choose the type of exit slip based on my assessment goals for the lesson, and then I study patterns in the resulting data to help me change my course of action when needed. Most importantly, I appreciate the opportunity to learn from and reflect upon valuable student input.

The Journey Begins

“Numeracy means the ability both to use numbers, arithmetically and algebraically, and to understand the concepts, relationships, and logic embedded in mathematical thought. A modern citizen cannot make critical judgments without these skills.”

-Ted Sizer, Horace’s Compromise

post